原文链接:http://www.juzicode.com/python-module-matplotlib-3d-plotting
Matplotlib的3D绘图工具扩展了数据可视化维度,支持创建三维曲面、散点图和柱状图等复杂可视化效果,适用于科学计算、工程模拟和空间数据分析等场景。
三维绘图应用场景
- 数学函数曲面可视化
- 流体动力学模拟
- 分子结构建模
- 地理高程数据展示
- 多变量数据关系分析
- 机械设计三维渲染
安装与导入
pip install matplotlib numpy
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np三维绘图方法
1)3D曲面图
可视化二元函数曲面特征。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
# 创建数据网格
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))
# 绘制曲面
surf = ax.plot_surface(X, Y, Z, cmap='viridis',
edgecolor='none',
rstride=1, cstride=1)
# 添加颜色条和标签
fig.colorbar(surf, ax=ax, shrink=0.5)
ax.set_title('三维正弦曲面')
ax.set_xlabel('X轴')
ax.set_ylabel('Y轴')
ax.set_zlabel('Z值')
plt.savefig('3d_surface.png', dpi=300)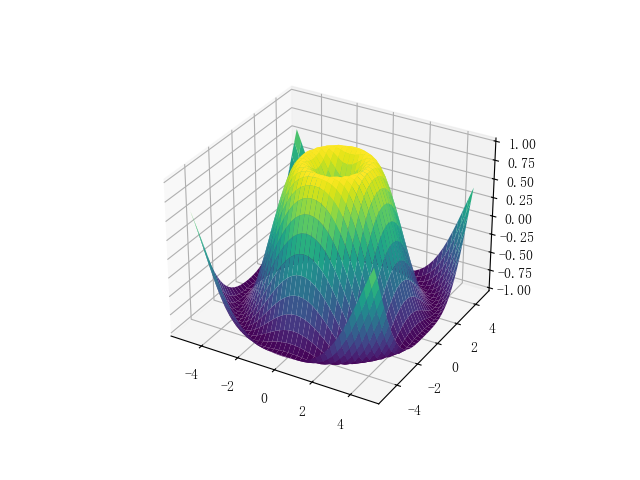
2)3D散点图
展示三维空间数据点分布。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(9, 6))
ax = fig.add_subplot(111, projection='3d')
# 生成随机数据
np.random.seed(42)
n = 500
x = np.random.randn(n)
y = np.random.randn(n)
z = np.random.randn(n)
colors = np.arctan2(z, y)
# 绘制散点
scatter = ax.scatter(x, y, z, c=colors,
cmap='plasma',
s=20, alpha=0.8)
# 添加图例和标签
ax.set_title('三维散点分布')
ax.set_xlabel('特征X')
ax.set_ylabel('特征Y')
ax.set_zlabel('特征Z')
ax.legend(*scatter.legend_elements(),
title="角度值")
plt.savefig('3d_scatter.png', dpi=300)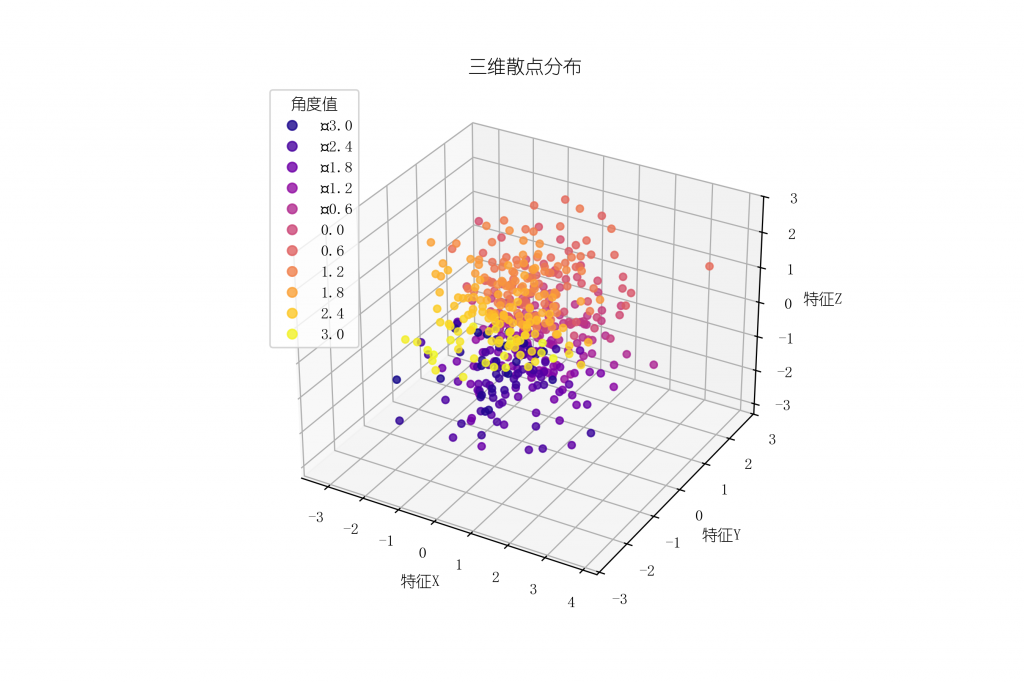
3)3D柱状图
展示二维分类数据的数值比较。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 定义分类数据
categories = ['A', 'B', 'C', 'D']
subcats = ['Q1', 'Q2', 'Q3']
colors = ['#FF6B6B', '#4ECDC4', '#FFE66D']
# 三维柱状位置
xpos = np.arange(len(categories))
ypos = np.arange(len(subcats))
xpos, ypos = np.meshgrid(xpos, ypos)
xpos = xpos.flatten()
ypos = ypos.flatten()
zpos = np.zeros_like(xpos)
# 柱状高度和数据
dx = dy = 0.5
dz = np.array([
3, 5, 2, 4,
6, 2, 7, 5,
4, 3, 6, 8
])
# 绘制柱状图
for i in range(len(dz)):
ax.bar3d(xpos[i], ypos[i], zpos[i],
dx, dy, dz[i],
color=colors[i % len(colors)],
shade=True)
# 设置坐标轴标签
ax.set_xticks(np.arange(len(categories)) + dx/2)
ax.set_yticks(np.arange(len(subcats)) + dy/2)
ax.set_xticklabels(categories)
ax.set_yticklabels(subcats)
ax.set_title('季度分类数据对比')
ax.set_xlabel('产品类别')
ax.set_ylabel('季度')
ax.set_zlabel('销售额(百万)')
plt.savefig('3d_bars.png', dpi=300)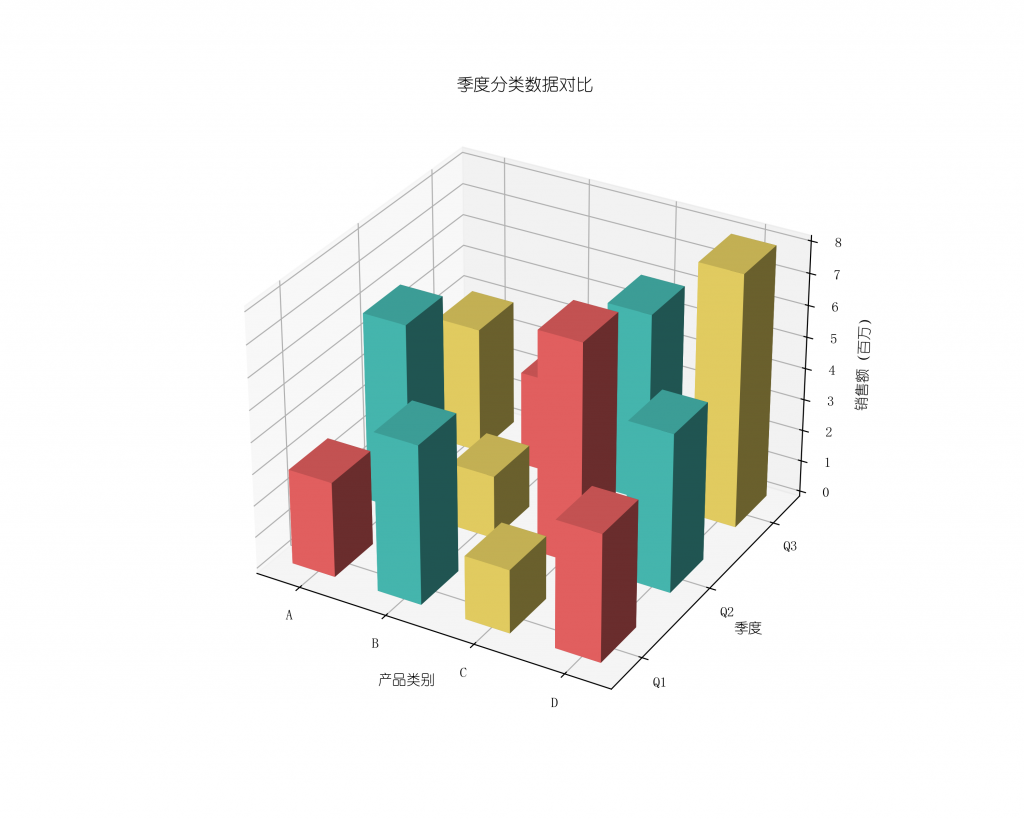
4)3D等高线图
三维曲面与二维投影结合展示。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 生成数据
X = np.linspace(-3, 3, 100)
Y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(X, Y)
Z = np.exp(-(X**2 + Y**2)) * np.cos(2*X)
# 绘制曲面和等高线
surf = ax.plot_surface(X, Y, Z, cmap='coolwarm',
rstride=2, cstride=2,
alpha=0.7)
ax.contourf(X, Y, Z, zdir='z', offset=-1, cmap='coolwarm')
# 添加标签和设置视角
ax.set_zlim(-1, 1)
ax.view_init(elev=30, azim=45)
ax.set_title('三维等高线图')
ax.set_xlabel('X轴')
ax.set_ylabel('Y轴')
ax.set_zlabel('Z值')
fig.colorbar(surf, shrink=0.5)
plt.savefig('3d_contour.png', dpi=300)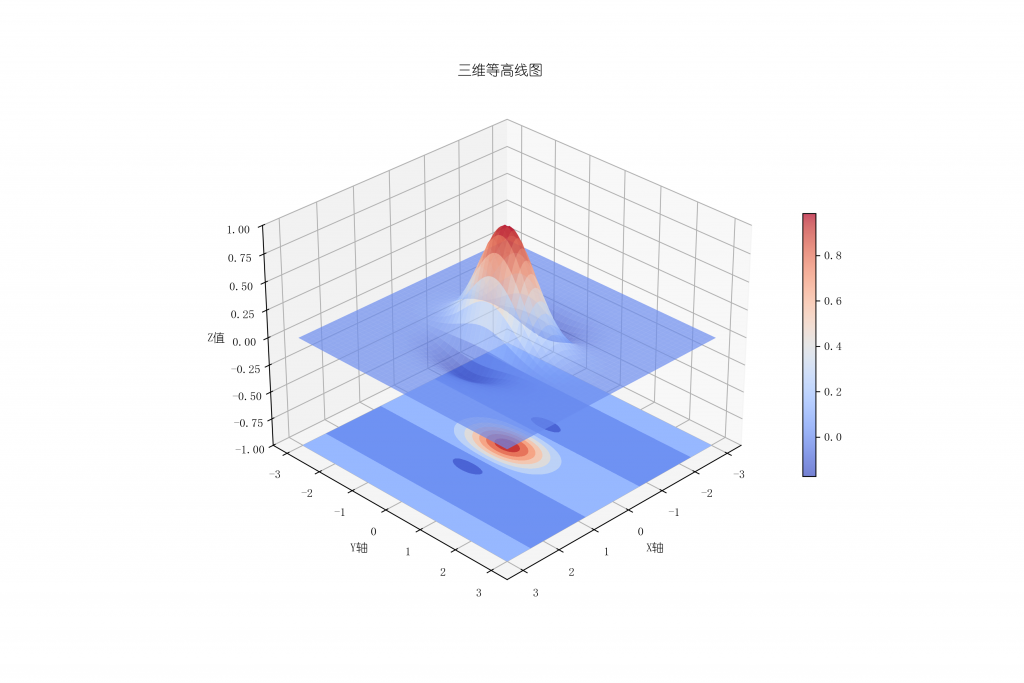
5)3D线框图
展示函数拓扑结构的骨架视图。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 创建数学曲面数据
X = np.linspace(-3, 3, 50)
Y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(X, Y)
Z = np.sinc(np.sqrt(X**2 + Y**2))
# 绘制线框图
wire = ax.plot_wireframe(X, Y, Z,
rstride=3, cstride=3,
linewidth=0.8,
color='#3498db')
# 添加辅助元素
ax.set_title('Sinc函数三维线框图', fontsize=14)
ax.set_xlabel('X轴', fontsize=10)
ax.set_ylabel('Y轴', fontsize=10)
ax.set_zlabel('Z值', fontsize=10)
ax.view_init(elev=25, azim=-45)
# 添加底部投影
cset = ax.contourf(X, Y, Z, zdir='z', offset=-0.5,
cmap='coolwarm', alpha=0.6)
plt.colorbar(cset, ax=ax, shrink=0.5, label='Z值')
plt.savefig('3d_wireframe.png', dpi=300, bbox_inches='tight')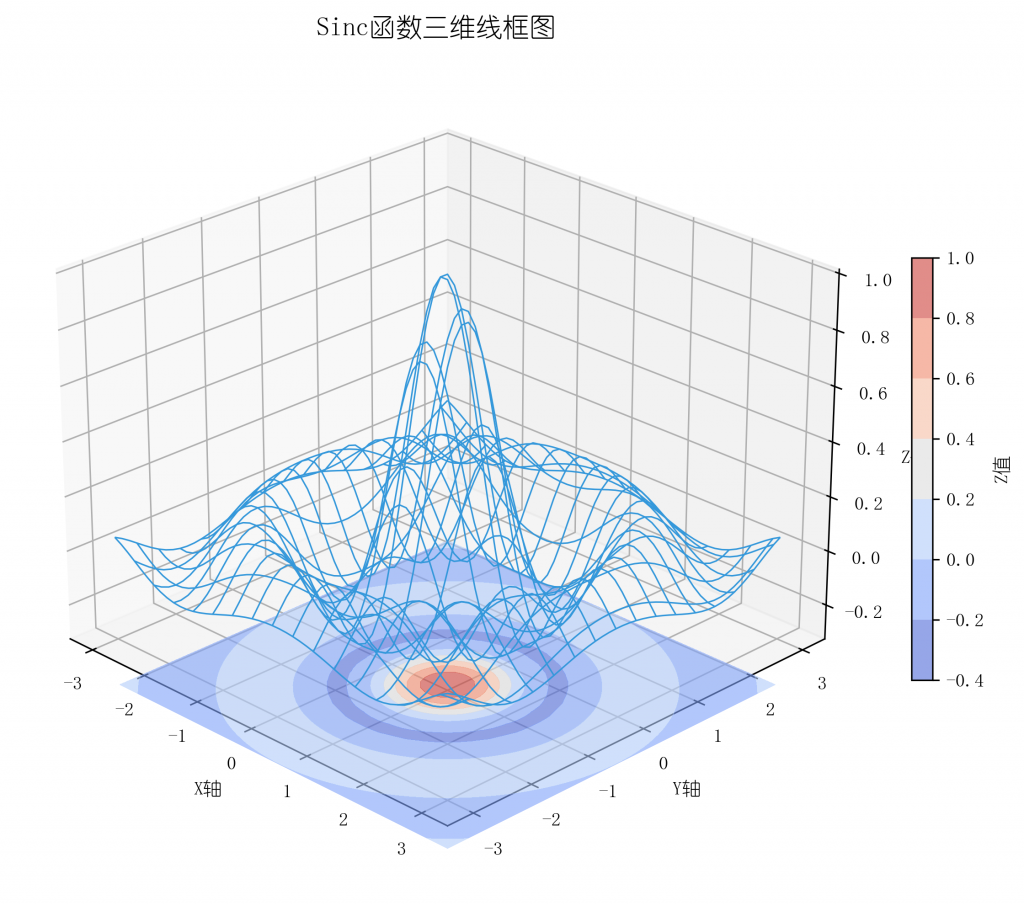
6)3D向量场图
可视化三维空间中的向量场分布。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(12, 9))
ax = fig.add_subplot(111, projection='3d')
# 创建网格点
x, y, z = np.meshgrid(np.arange(-2, 2, 0.5),
np.arange(-2, 2, 0.5),
np.arange(-2, 2, 0.5))
# 定义向量场函数
u = -y - z
v = x + 0.2*y
w = 0.2 + z*(x - 3)
# 绘制三维向量场
quiver = ax.quiver(x, y, z, u, v, w,
length=0.3,
normalize=True,
color='#e74c3c',
arrow_length_ratio=0.3)
# 设置图表属性
ax.set_title('三维向量场可视化', fontsize=15)
ax.set_xlabel('X轴', fontsize=10)
ax.set_ylabel('Y轴', fontsize=10)
ax.set_zlabel('Z轴', fontsize=10)
ax.set_xlim([-2, 2])
ax.set_ylim([-2, 2])
ax.set_zlim([-2, 2])
# 添加参考平面
xx, yy = np.meshgrid(np.linspace(-2, 2, 10),
np.linspace(-2, 2, 10))
zz = np.zeros_like(xx)
ax.plot_surface(xx, yy, zz, alpha=0.2, color='gray')
plt.savefig('3d_vector_field.png', dpi=300)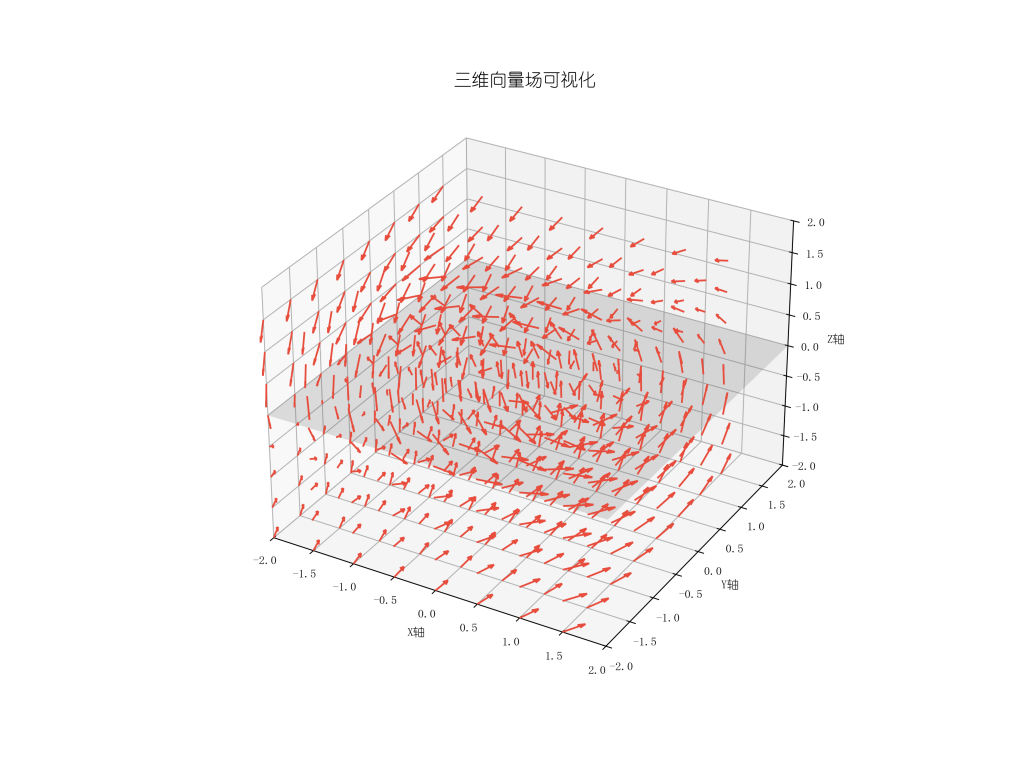
7)3D曲面填充图
创建具有透明度的分层曲面可视化。
# juzicode.com/VX公众号:juzicode
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['YouYuan']
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
# 创建基础曲面
theta = np.linspace(0, 2 * np.pi, 100)
r = np.linspace(0, 3, 50)
T, R = np.meshgrid(theta, r)
X = R * np.cos(T)
Y = R * np.sin(T)
Z1 = np.sin(R) * np.cos(T*2) + 1
Z2 = np.cos(R) * np.sin(T) - 1
# 绘制半透明曲面
surf1 = ax.plot_surface(X, Y, Z1,
alpha=0.7,
cmap='viridis',
antialiased=True)
surf2 = ax.plot_surface(X, Y, Z2,
alpha=0.5,
cmap='plasma',
antialiased=True)
# 添加等高线投影
ax.contour(X, Y, Z1, zdir='z', offset=-2.5,
cmap='viridis', linewidths=1)
ax.contour(X, Y, Z2, zdir='x', offset=-4,
cmap='plasma', linewidths=1)
# 设置图表属性
ax.set_zlim(-2.5, 2.5)
ax.set_title('分层透明曲面可视化', fontsize=16)
ax.set_xlabel('X轴', fontsize=10)
ax.set_ylabel('Y轴', fontsize=10)
ax.set_zlabel('Z值', fontsize=10)
ax.view_init(elev=30, azim=35)
# 添加颜色条
fig.colorbar(surf1, ax=ax, shrink=0.5, label='上层曲面')
fig.colorbar(surf2, ax=ax, shrink=0.5, label='下层曲面')
plt.savefig('3d_transparent_surfaces.png', dpi=300, transparent=True)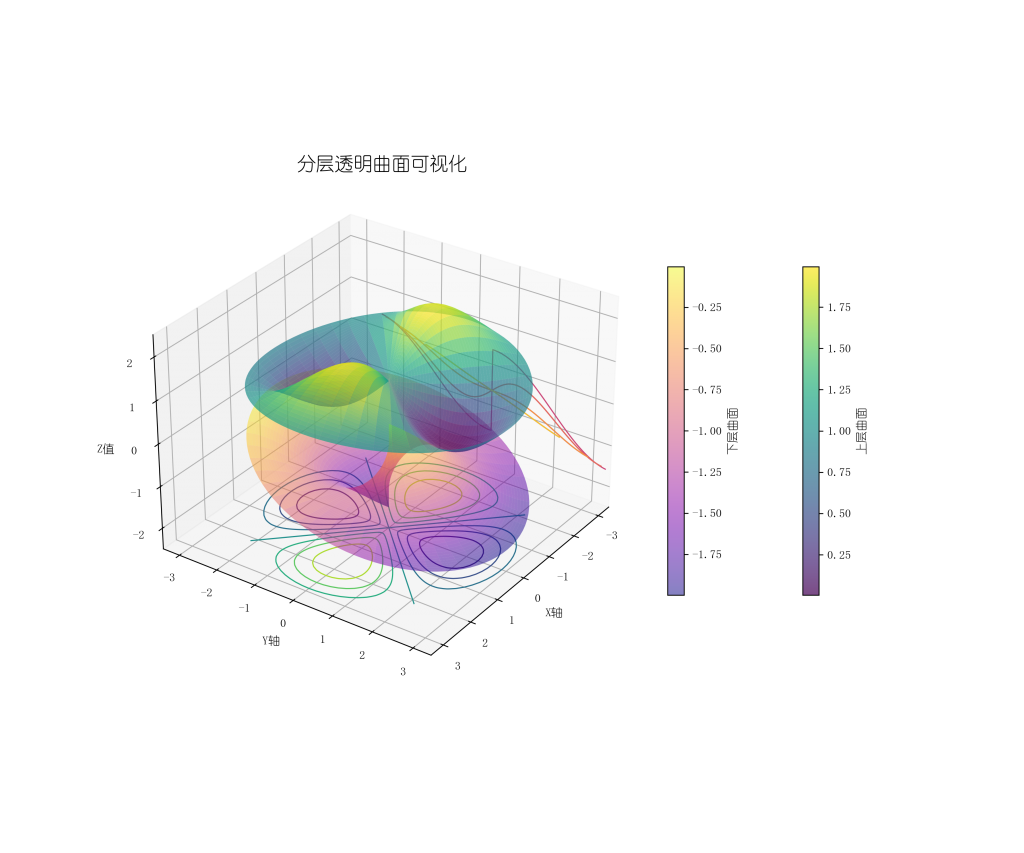
三维绘图技巧总结
核心优势:
- 支持曲面/散点/柱状/线框/等高线等10+种3D图表
- 完整的视角控制(俯仰角/方位角)
- 与NumPy深度集成处理三维数据
- 可导出矢量格式用于科研论文
注意事项:
- 使用
fig.add_subplot(111, projection='3d')创建3D坐标轴 - 大数据集开启
rstride和cstride参数优化性能 - 通过
view_init(elev, azim)调整观察视角 - 导出PNG时推荐dpi≥300保证清晰度
- 复杂场景考虑使用Mayavi进行高性能渲染
